a) What is the worst-case complexity of each of the following code fragments? (Unit 1)
i) Two Loops in a row:

for (i = 0; i < N; i++) {
    Sequence of statements
}
for (j = 0; j < M; j++) {
    Sequence of statements
}
                        

for (i = 0; i < N; i++) {
    for (j = 0; j < N; j++) {
        Sequence of statements
    }
}
for (k = 0; k < M; k++) {
    Sequence of statements
}
                        

b) What is ADT? Compute the addresses of a 3-D array in a row and column major form? (Unit 1)

c) Write Prim's algorithm to get minimal spanning tree out of a graph? (Unit 4)

a) Consider the following function that takes reference to head of a Doubly Linked List as parameter. Assume that a node of doubly linked list has previous pointer as prev and next Pointer as next. (Unit 1)

Void fun (struct node ** head-ref)
{
    struct node * temp=NULL;
    struct node * current= *head-ref;
    while(current !=NULL)
    {
        temp=current->prev;
        current -> prev =current -> next;
        current->next=temp;
        current = current -> prev;
    }
    if (temp!=NULL)
        *head_ref=temp->prev;
}
                        

b)
i) Transform the following expression in Postfix Notation:
$A + (B + D) / E - F * (G + H/K)$ (Unit 2)
ii) Evaluate the following postfix expression:
$ABC * D/+$ where $A = 2, B = 3, C = 4, D = 6$ (Unit 2)

a) Write an algorithm to enque and deque an element in a queue? The queue implementation using a linked list? (Unit 2)

b) Insert the following data keys in the AVL Tree:
16, 23, 9, 163, 64, 29, 73, 83, 90, 96 (10 keys) (Unit 3)

a) The in-order and pre-order traversal sequence of a node in a binary tree are given below:
In-order: E A C K F H D B G
Pre-order: F A E K C D H G B
Draw the binary tree. State briefly the logic used to construct the tree. (Unit 3)

b) Describe the performance of the algorithms used to multiply two N $\times$ N matrices using suitable measures of complexity. You should make clear what operations you are counting, what is the worst-case that you are considering, (and, perhaps, average-case, and best-case, where appropriate). Also consider space complexity? (Unit 1)

a) i) Sort the following data in ascending order using Quick sort:
9, 4, 12, 6, 5, 10, 7 (Unit 5)
ii) Prove that Heap sort, Merge sort, Quick sort takes O (n log n) time in the worst case? (Unit 5)

b) Apply Binary Search to find 123 in the following list:
49, 98, 101, 123, 149, 194, 199, 211, 240, 286, 840, 930 (12 data) (Unit 5)

a) Is there any difference between threaded and unthreaded binary tree? What is a B-tree? Explain. (Unit 3)

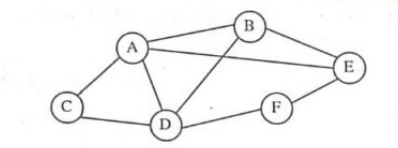
b) For the graph shown below find the following:
i) Adjacency list representation
ii) Adjacency matrix representation
iii) Adjacency multi list representation (Unit 4)

a) What do you mean by tower of Hanoi Problem? Explain with suitable example along with diagram? (Unit 2)

b) Write algorithms for DFS and BFS traversal on a graph. (Unit 4)

Given the values {2341, 4234, 2839, 430, 22, 397, 3920} a hash table of size 7 and a hash function $h(x) = x \mod 7$, show the resulting table after inserting the values in the given order with each of the following collision strategies. (Unit 5)
i) separate chaining
ii) linear probing
iii) double hashing with second hash function $h_1(x) = (2x - 1) \mod 7$